If you are seeing this message, it is because
you are using an old browser (perhaps Netscape 4.x) that has poor support
for contemporary Web standards (and cascading style sheets in particular),
OR it is because you have neglected to download this page's style
sheet,
style.css. As a result, you will be seeing
a largely unformatted version of this Web page, and will be missing a great
deal of information conveyed by that formatting. My suggestion:
Download
and install a more recent browser. Internet Explorer 6, Netscape 7,
and Mozilla are all good choices.
Java's Primitive Types Revisited
Table of Contents
-
Random Access Memory
-
Binary Counting
-
Binary Addition
-
The Convenience of Types
-
The Integer Types
-
The Floating-Point Types
-
The Analysis of Floating-Point Types
-
Exercises
These notes are meant to assist your understanding of the ways in which
the Java Virtual Machine uses your computer's memory to store data. They
specifically address the storage of boolean, integer, and floating-point
data. Storage of object data, such as for a Java String,
is a more complex issue, and one that is beyond the scope of this course.
Back to Contents
Random Access Memory
Random access memory (RAM) is the name given to the collection
of solid-state storage devices in your computer (Figure 1). 
Figure 1: A RAM module. Your computer likely contains two or three
of these. The width of this module is 13cm. (Photograph courtesy of freepctech.com.)
It is distinct from, for example, disk storage, in that it is volatile:
Its content is not preserved when power is removed (i.e., when you shut
your computer off).
RAM is constructed of a great many bit devices, each capable
of "remembering" from one moment to the next whether it is "on" – represented
by a 1 – or "off" – represented by a 0. ("Bit" is a contraction of "binary
digit, meaning a 0 or a 1.) For reasons of efficiency, these bit
devices are grouped into collections of, typically, 32-bit words,
and each word is uniquely identified by a hard-wired numeric address.
These addresses are sequentially assigned: The lowest address is 0, and
the highest n - 1, where n is the number of bit devices divided
by the word size for your computer. A PC with 512 megabytes (MB) of RAM
has memory addresses 0 through 134217727 available to it. (A byte is 8
bits; 1MB is 10242 bytes.) A device called a memory
controller acts as an intermediary between RAM and other devices in
your computer, notably the central processing unit (CPU), which is responsible
for executing program code. The memory controller stores (writes) and retrieves
(reads) data to and from RAM in response to requests from these other devices.
The memory controller can gain access to any word in RAM directly by way
of its address. The term "random access" is meant to imply that, given
any two words selected at random, access times for both are the same.
Back to Contents
Binary Counting
This section introduces one way in which a program can treat a collection
of bits in RAM as representing some value other than 0 or 1. The representation
is for integers, but unlike most of Java's primitive types, it will be
unsigned, meaning it can only be used to represent positive integer
values. Java's smallest integer type uses eight bits. For simplicity, this
example uses only four.
To work with this type, called the nybble (pronounced "nibble" –
an archaic, but actual term for a 4-bit device), the programming language
arbitrarily ascribes a column value to each of the bits, as follows:
At this point, a comparison with our usual system of counting is in order.
We count in a system called decimal, using the value ten as a number
base. Thus when we write a number, each column value is a power of ten,
as in this example for the number eight thousand, nine hundred and three:
So, counting in base two, or binary, is similar, but for the fact
that since our largest digit is 1 and not 9, our columns represent powers
of two, and not ten. The value of a nybble,
then, is the sum a(23) + b(22)
+ c(2) + d, where each of a, b, c, and
d is either a 0 or a 1. Here is how we count up to fifteen in binary
(equivalent decimal values shown on the right):
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
1 |
1 |
| 0 |
0 |
1 |
0 |
2 |
| 0 |
0 |
1 |
1 |
3 |
| 0 |
1 |
0 |
0 |
4 |
| 0 |
1 |
0 |
1 |
5 |
| 0 |
1 |
1 |
0 |
6 |
| 0 |
1 |
1 |
1 |
7 |
| 1 |
0 |
0 |
0 |
8 |
| 1 |
0 |
0 |
1 |
9 |
| 1 |
0 |
1 |
0 |
10 |
| 1 |
0 |
1 |
1 |
11 |
| 1 |
1 |
0 |
0 |
12 |
| 1 |
1 |
0 |
1 |
13 |
| 1 |
1 |
1 |
0 |
14 |
| 1 |
1 |
1 |
1 |
15 |
A type defines a finite set of values. The set is finite, because a type
works with a fixed number of bits. The number of possible permutations
of bit values in an n-bit entity is 2n
(that's 24 == 16 for a nybble), and each bit pattern
represents a unique value in the set. The same holds true for each of Java's
primitive types, though most do not interpret bit patterns exactly in the
manner I've described above for the nybble.
Back to Contents
Binary Addition
Computer addition of two binary integer values is done in a manner that
should be familiar to anyone who can add columns of numbers by hand. The
addends (i.e., the two numbers to be added together) are aligned
by column. Then, working from the least significant (rightmost) column
toward the most significant column, corresponding digits from the addends
are summed. If a column sum results in 10 (binary or decimal), the 1 is
carried, and added to the sum of the digits in the next most significant
column. Keep in mind, however, that the values a computer works with are
binary, not decimal, and its addends and sums have predetermined bit lengths.
Moreover, all those bits are in use at all times, even if the most significant
bits are 0s. Consider these two examples, the first in familiar decimal,
the second in binary. Carried values are shown in dotted borders.
| 1 |
1 |
1 |
|
|
| 0 |
7 |
8 |
9 |
789 |
| 0 |
4 |
1 |
3 |
+413 |
| 1 |
1 |
1 |
|
|
| 0 |
1 |
1 |
1 |
7 |
| 0 |
1 |
0 |
1 |
+5 |
Note that a carry out of the most significant column may occur, as depicted
here:
| 1 |
1 |
1 |
1 |
|
|
| |
1 |
0 |
1 |
1 |
11 |
| |
0 |
1 |
1 |
1 |
+7 |
|
| |
0 |
0 |
1 |
0 |
2 |
The sum should, of course, be 18 decimal, or 10010 binary, but since the
representation I'm using for the sum is restricted in size to four bits,
I end up getting 18 % 24 == 2 decimal, or 10 binary.
This condition is called overflow, and computers typically have
built in hardware to detect when it has occurred.
Back to Contents
The Convenience of Types
Thanks in part to certain features of CPU's, but mostly to our use of a
high-level programming language (Java), we can usually get away with pretending
that the computer has no more trouble dealing with a double
than it has dealing with an int.
Yet while the latter happens to occupy a 32-bit word exactly, the former
is a 64-bit entity. So, although the double
is stored across two memory locations and not one, the work of deciding
how the number should be split up for storage is handled for us by the
compiler. This masking of detail is a tremendous convenience for the modern
programmer, who, unlike his or her unlucky predecessors in the 1940s and
1950s, can get on with the work of designing elegant algorithms, and let
the compiler take care of messy, behind-the-scenes details of memory addressing.
However, a programmer ignores computer architecture at her or his peril:
Understanding the limitations of a type definition can often help us to
understand what might otherwise seem to be inexplicable behaviour in a
program. The sections below describe the internal representations used
for data items of Java's primitive types: The boolean
type, the char type, the integer
types, and the floating-point types. Of these, we have only made (and will
continue to make) consistent use of the boolean, int,
and double types. The others are described
here for completeness. These notes also also introduce a fictional floating-point
type as an illustrative model.
Back to Contents
The boolean Type
A boolean value occupies 1 bit. The false
and true values we assign to them are mapped,
internally, to 0 and 1, respectively.
Back to Contents
The char Type
The reason we try to avoid using char type
values in APSC142 is their annoying habit of sometimes appearing as alphabetic
characters, and at other times as positive integer values. To see this,
place the statements,
System.out.println ('A');
System.out.println ('B');
System.out.println ('A' + 'B');
in your next Java program. (Note that, unlike String
constants in Java, char constants appear
in single quotes.)
A char value occupies 16 bits. It represents
an unsigned integer value that is meant to be used as an index into a table
of viewable characters. Java conforms to the internationally-recognized
Unicode standard for character representations. It must be understood that
the value stored in RAM for a given character bears no resemblance to the
form of the character on the screen or in print. The fact that sending
the char value 'A'
to the display with a System.out.println()
statement (usually) results in a letter "A" of some font appearing for
the user is thanks to a combination of your computer's operating system
working in concert with your video hardware. By the way, in Unicode, 'A'
is represented internally by 65, and 'B'
by 66, which might help to explain the output from the third program statement
given above. To learn more about Unicode, visit www.unicode.org.
Back to Contents
The Integer Types
It has already been noted that char is an
integer type, of sorts. In fact, char is
the only numeric type in Java that is unsigned. All the others are signed
representations, meaning that their sets of possible values contain both
negative and positive numbers. The integer primitive types, byte, short, int,
and long, represent patterns
of 8, 16, 32, and 64 bits, respectively. As each representation uses its
bits in the same way, an examination of the byte
will suffice to illustrate the rest.
It should be clear by now that whatever interpretation
one puts on a collection of 8 bit values, there can never be more than
28, or 256 of them. So, if a byte
is to use half of these bit patterns to represent negative values (those
less than 0), and the other half to represent positive values (those greater
than or equal to 0), then the largest set of integers it can represent
is {-128 .. 127}. Bit patterns are mapped to values according to a scheme
called two's complement, already widely in use among programming
languages when Java was created. All of Java's integer types use two's
complement. For a byte, the bit patterns
are as follows:
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-128 |
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-127 |
| 1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
-126 |
| 1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
-125 |
| 1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
-124 |
| · |
· |
| · |
· |
| 1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
-3 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
-2 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
-1 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
| 0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
2 |
| 0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
3 |
| · |
· |
| · |
· |
| 0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
123 |
| 0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
124 |
| 0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
125 |
| 0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
126 |
| 0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
127 |
Some things to note about two's complement:
-
The value of the most significant (left-most) bit is 1 for negative values,
and 0 for positive values. This bit position is often called the sign
bit for this reason.
-
127 + 1 == -128. You may confirm this by using the binary
addition technique described above. In fact, any pair of byte
addends that should give a sum greater than 127 will, in a byte
representation, give a negative sum. This is a special form of overflow
condition in which the sign bit is changed inappropriately. Java does not
treat this as an error, which has serious implications for programmers.
Consider for example the following:
System.out.println ("Byte values:");
for (byte i = -128; i <= 127; i++)
System.out.println (i);
It might seem that this should print out all the elements in the set
of byte, and then get on with something
else, but in fact the for is an infinite
loop. To see why that's so, consider the while
loop equivalent:
{
byte i = -128;
while (i <= 127)
{
System.out.println (i);
i++;
}
}
Note that when i reaches 127,
the while loop's statement block executes
for the 256th time, which means that after the System.out.println
(i) occurs, so does the i++, and
the bits in i "roll over"
to the pattern for -128. (This is true in the for
version of the loop as well.) When the boolean expression, i
<= 127, is evaluated immediately afterwards, it is still true,
since -128 is less than or equal to 127. As a consequence, the looping
starts all over again.
Back to Contents
The Floating-Point Types
The Java float and double
types are designed to comply with, respectively, the IEEE Standard 754
for single- (32-bit) and double-precision (64-bit) floating-point numbers.
The rules governing these representations are quite complicated, and as
a result, floating point arithmetic is usually handled by a specialized
sub-processor within (or near to) a computer's CPU. Java is by no means
unique in adopting Standard 754, but you may come across older programming
languages in your careers that use different schemes to represent real
numbers.
As an aid to understanding the 32-bit float
and the 64-bit double types, these notes
introduce a model floating-point type called minifloat.
It is meant to be what the IEEE would have proposed for Standard 754, had
it felt the need for an 8-bit type.
The minifloat consists of three arbitrary
fields of bits, as shown here:
Bits are assigned to specific purposes as follows:
Each of these terms is explained below.
Back to Contents
The Sign Bit
If the sign bit is 0, the quantity expressed by the remaining bits is considered
positive. If the sign bit is 1, the quantity is negative.
Back to Contents
The Exponent
The 3-bit exponent requires more explanation. It represents a signed integer
value, but the scheme used is not two's complement,
as is the case for Java's integer types. Instead it uses a representation
called excess-3. This representation maps bit patterns to integer
values as follows:
| 0 |
0 |
0 |
-3 |
| 0 |
0 |
1 |
-2 |
| 0 |
1 |
0 |
-1 |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
2 |
| 1 |
1 |
0 |
3 |
| 1 |
1 |
1 |
4 |
The representation is called excess-3, not because of the number of bits
used, but because the unsigned value of each bit pattern is three greater
than its decreed value. Note, for example that 011, which has an unsigned
value of 3, is used to represent 0. By contrast, the 32-bit float
has an 8-bit exponent stored as an excess-127 value, and the 64-bit double
has an 11-bit exponent stored in excess-1023.
The reason for greying-out the 000 and 111 bit patterns in the table
above, is that they are reserved for special cases, as you shall see. This
means that the exponent field has an effective range of only -2 .. 3. The
implied base for the exponent is, perhaps not surprisingly, 2.
Back to Contents
The Mantissa
In most cases, the 4-bit mantissa is actually considered to be 5 bits in
length. The missing bit, appropriately called the hidden bit, isn't
stored because it is always assumed to have the value 1. This drawing shows
the mantissa with the hidden bit in place and the column values assigned
to each bit:
You can imagine that there is an unseen "binary" point (as opposed to a
decimal point) sitting between the 20
and the 2-1 position, separating the whole number
and fractional parts of the mantissa.
We can list all possible values of the mantissa (and their decimal equivalents)
as follows:
| 1 |
0 |
0 |
0 |
0 |
1.0 |
| 1 |
0 |
0 |
0 |
1 |
1.0625 |
| 1 |
0 |
0 |
1 |
0 |
1.125 |
| 1 |
0 |
0 |
1 |
1 |
1.1875 |
| 1 |
0 |
1 |
0 |
0 |
1.25 |
| 1 |
0 |
1 |
0 |
1 |
1.3125 |
| 1 |
0 |
1 |
1 |
0 |
1.375 |
| 1 |
0 |
1 |
1 |
1 |
1.4375 |
| 1 |
1 |
0 |
0 |
0 |
1.5 |
| 1 |
1 |
0 |
0 |
1 |
1.5625 |
| 1 |
1 |
0 |
1 |
0 |
1.625 |
| 1 |
1 |
0 |
1 |
1 |
1.6875 |
| 1 |
1 |
1 |
0 |
0 |
1.75 |
| 1 |
1 |
1 |
0 |
1 |
1.8125 |
| 1 |
1 |
1 |
1 |
0 |
1.875 |
| 1 |
1 |
1 |
1 |
1 |
1.9375 |
Back to Contents
Combining the Sign Bit, the
Exponent, and the Mantissa
The value of a floating point number is usually taken to be:
-1signBit × mantissa
× 2exponent
which, as you can probably tell, is a binary form of scientific notation.
Consider, for example, the following bit pattern as the representation
of a minifloat:
Its value for computation is:
| -1 |
1 |
× |
1 |
0 |
1 |
0 |
0 |
×2 |
0 |
1 |
0 |
If you refer to the exponent and mantissa equivalence tables, above, you
will find this to be equal to:
-11 × 1.25 × 2-1
== -0.625
Back to Contents
Special Cases
To address several limitations of the floating-point structure described
thus far, a number of bit patterns are deemed to have special meaning.
These involve the reserved exponent bit patterns referred to above (i.e.,
all 0's and all 1's), and are as follows:
-
Zero
The most obvious weakness of the floating-point structure as described
above, with its hidden bit always assumed to be 1, is its inability to
represent 0.0. This is solved by decreeing that a floating-point number
with an all-0s exponent field and an all-0s mantissa field has the value
0.0. This introduces a new potential source of confusion, as the sign bit
is free to be either 0 or 1, giving
According to the rules laid out by the IEEE for floating-point formats,
-0.0 == 0.0 must be true. They are distinct values, however, as can be
demonstrated using Java output:
double x = 0.0; // Zero
double y = -0.0; // Negative zero
if (x == y)
System.out.println (x + " and " + y
+ " are equal, but different.");
else
System.out.println (x + " and " + y
+ " are not equal.");
The existence of "negative zero" in IEEE Standard 754 suggests that it
is no great cause for concern, though it highlights for us the arbitrariness
of number representation in computers.
-
Denormalized numbers
Most floating point numbers are normalized, which is to say
the mantissa has a one-digit integer portion, that being the hidden bit,
which is always considered to have the value 1. However, if the exponent
bits are all 0, and the mantissa non-zero, then the mantissa is considered
to be a denormalized fractional number. There is no hidden bit implied
in a denormalized number, and the values of the columns are chosen so that
the largest denormalized number, by magnitude (i.e., ignoring the value
of the sign bit), is just smaller than the smallest normalized number.
For a minifloat, the smallest
normalized number, by magnitude, is
The mantissa column values for a denormalized minifloat
are arbitrarily reassigned as follows:
So that the largest denormalized value, by magnitude, is:
| 1 |
1 |
1 |
1 |
0.234375 |
| 2-3 |
2-4 |
2-5 |
2-6 |
This is, indeed, just smaller than 0.25. The range of denormalized numbers,
excluding ±0.0 (which are special cases of denormalized numbers)
for a minifloat is
±0.015625 .. ±0.234375
It is important to bear in mind, when considering this range, that it
contains only 16 positive and 16 negative values. The increment between
those values is exactly 1/(2-6),
or 1/64. Since denormalized numbers have the smallest non-zero values,
by magnitude, of all the floating-point numbers, any value smaller than
the smallest is considered to have value 0.0 (or -0.0).
-
Infinity
If the exponent bits of a floating-point number are all 1s and the
mantissa bits all 0s then the value is deemed to be an infinity. The value
of the sign bit distinguishes positive (0) from negative (1) infinity.
Infinity is the result of any operation on a floating-point number that
exceeds its maximum or minimum values. For a minifloat,
the maximum value is 15.5, and the minimum value is -15.5.
-
NaN
If the exponent bits of a floating-point number are all 1s and one
or more mantissa bits are also 1 (excluding the hidden bit), then the value
is deemed to be Not a Number (NaN). A NaN value is an indicator that a
floating-point operation failed. For example:
double d = Math.sqrt (-1.0);
On execution of this statement, the variable d
would have the value NaN.
There are, according to IEEE Standard 754, two categories of NaN (called
QNaN and SNaN), distinguishable from one another by the value of the most-significant
mantissa bit. However, Java only uses one internal representation for NaN.
The sign bit has no apparent significance for a NaN.
Back to Contents
Analysis of Floating-Point Numbers
There is a partial implementation of the minifloat
data type as a Java class, Minifloat.java
as well as a test program, TestMinifloat.java,
to try it out. (Download and save both files to the same directory.) TestMinifloat
lists the bit patterns and corresponding floating-point values for all
the minifloat numbers. If you copy the range
of positive (non-infinite) values into an Excel spreadsheet, and make a
scatter plot chart mapping the bit patterns as positive integers on the
x axis, and the floating point values on the y axis, the following is the
result:
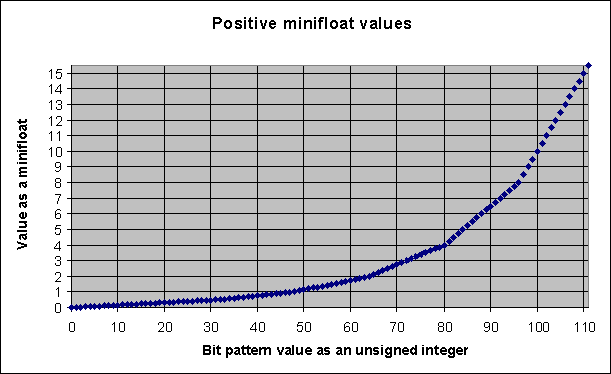
As you can see, the assignment of bit patterns to floating-point values
is not linear (although segments of the chart are linear). In fact, although
the minifloat representation can approximate
real values from -15.5 .. 15.5, most have a value in the range -2.0 ..
2.0. The gaps between representable values increase with magnitude, so
the ability to represent large numbers, in addition to small numbers, comes
at the expense of precision. On the other hand, if the programming task
at hand has us working with very large numbers, chances are we won't worry
that the machine doesn't necessarily distinguish between very large value
n and slightly larger value n + 1. Where precision does
matter, as with financial applications, it is probably best to work with
integer representations (e.g., counting pennies instead of dollars).
Gaps between small values can also be problematic. Note, for example,
that the value 0.1 decimal (i.e., one-tenth) has no binary floating-point
representation. The reason for this is that no sum of fractional powers
of two add up to 0.1 decimal. To see that this is so, place the following
code in the context of a Java program:
double sum = 0.0;
System.out.println ("Counting up to 1 in tenths:");
while (sum != 1.0)
{
sum = sum + 0.1;
System.out.println (sum);
if (sum > 1.0)
{
System.out.println ("Whoops! Missed it!");
break;
}
}
The fact that Java displays "0.1" for the real value 0.1 decimal shows
that its double-to-String
conversion routine does some rounding or truncating. While there may be
advantages of this behaviour, it seems odd that 2 * 0.1 displays as "2.0",
but 3 * 0.1 displays as "0.30000000000000004".
Back to Contents
Exercises
Here are some problems that you may attempt, to test your understanding
of the concepts presented in these notes.
Two's Complement: Give solutions in 16-bit binary and in decimal
-
What are the maximum and minimum values that can be assigned to a Java
variable of type short (a 16-bit two's complement
number)?
-
What is the result of adding 1 to a short
of maximum value? (Give the value, don't just write, "Overflow").
-
What is the result of subtracting 1 from a short
of minimum value? (Give the value. If you can't work out for yourself how
subtraction might be done on binaries, just try adding the bit pattern
for -1).
Floating-Point
-
The machine epsilon of a floating-point representation is a measure
of its ability to distinguish between numbers of close but different values.
It is the smallest positive value, e, such that 1 + e > 1.
For the floating-point numbering systems in Java (and for the minifloat),
it is defined as 21 - n, where n
is the number of mantissa bits, including the hidden bit. Find the machine
epsilon values for the following types. Give your answers as a power of
2. The first is done for you.
-
minifloat: Machine epsilon is 21
- 5 == 2-4
-
float
-
double
-
Write a Java program that finds and prints machine epsilon for a double.
This can be done as follows:
-
Set epsCandidate to 1.0
-
Set eps to 0.0
-
Loop
-
Exit when 1.0 + epsCandidate is equal to 1.0
-
Set eps to epsCandidate
-
Divide epsCandidate by 2.0
-
Send eps to output (i.e., the display)
Keeners should note that if a count variable (initially set to 0)
is incremented in the loop, the number of mantissa bits, including the
hidden bit, can also be determined this way.
-
Explain the output of this Java program:
public class ImportanceOfOperandOrdering
{
public static void main (String[] args)
{
System.out.println (1.0 + 1.0 + 1.0e17 - 1.0e17);
System.out.println (1.0e17 - 1.0e17 + 1.0 + 1.0);
}
}
Back to Contents
Original Author: Richard Linley
Revised by Jim Rodger
Last Updated: Fall 2003


