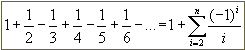
In the Dr. Seuss classic The Cat in the Hat Comes Back, having created a mess, the Cat in the Hat needs to clean it up. He can't clean up the mess himself, so needing help he lifts his hat and out pops Little Cat A, a smaller version of the Cat in the Hat. Little Cat A, in turn, also decides more help is needed, and lifts his hat to reveal Little Cat B. The process of each cat producing another, otherwise identical, but smaller copy continues until Little Cat Z arrives and is able to clean up the mess. Having finished the job, the cats return, in reverse order, into the hats.
Surprisingly, this process is a good example of the typical use of recursion in computer programming. The problem is decomposed into otherwise identical, but progressively smaller versions until it is small enough to be trivial, and the versions can end in reverse order, smallest to largest, each providing its solution to the next larger.
Once we've seen how recursion applies to our programs, we'll examine some examples of well-known recursive algorithms. We'll also show how problems can arise from poorly coded or inappropriate use of recursion.
As programmers, we write recursive method definitions: methods that include in their statements calls of themselves. While that may sound strange, it is actually quite useful for writing elegant solutions to many problems. Consider the factorial function, f(n) = n!, defined inductively by the following properties:
0!= 1
1!= 1·(0!) = 1
2!= 2·(1!) = 2
3!= 3·(2!) = 6
4!= 4·(3!) = 24
:
(n+1)!= (n+1)·(n!)
The first line indicates a base or non-recursive case for the function.
The last line indicates the algebraic pattern (recursion relation) that
permits (n+1)! to be computed after n! has been. Given the pattern, it
is easy to generalize to any positive integer. We can reformulate the definition
to focus on the "base case" and the general pattern. The factorial of a
non-negative integer n is given by:
1 if n = 0
otherwise n ·(n-1)!
Definitions with this form have two parts. The first specifies a base case, that is not recursive, but gives the element from which other elements may be derived, or constructed. The second specifies the rule for deriving other elements. This rule defines each new element in terms of an element that has already been derived. This is the recursive aspect of the definition. Such a definition translates naturally into the code for a Java method definition containing a selection statement with 2 branches, one corresponding to each part of the definition. Here's an example.
public static int fact (int n)
{
if (n == 0)
return 1;
else
return n*fact(n - 1);
}
What happens when the fact() method is called? Well, if n is 0
it executes the code corresponding to the base case, and simply returns
1, the defined value of 0!. If n is greater than 0, it executes code corresponding
to the recursive part of the definition. It multiplies n times the result
of computing factorial of n-1. This branch includes the recursive call
of the method, but with an argument one less than what it was called with.
This process will end when the argument to the recursive call is 0.
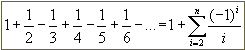
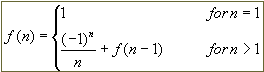
public static double sumTerms (int n)
{
if (n == 1)
return 1.0;
else
return (Math.pow(-1, n) / n) + sumTerms(n - 1);
}
Function definitions in this form are usually easy to translate into method
definitions that implement what is referred to as "tail recursion". If
the base case has been reached, the method returns a value directly, otherwise
it returns a value derived from the current argument value and a recursive
call with an argument value closer to the base case than the current value.
These method definitions end with a recursive call.
Both the fact() and sumTerm() methods illustrate tail recursion. In this form, the recursive call is the last operation of the method. The outcome is that when the method is executing, as each recursive call ends, the preceding one then also ends, and so on. Of course, it is possible for the recursive call to be located elsewhere in the method. In particular, there may be other operations in the definition, following the recursive call. If so, these operations will be performed only after all the recursive calls have been made and the base case reached. Then, the operations/statements following the recursive call in each method invocation will execute in succession, as the recursive calls terminate.
Here is the definition of a simple recursive method that does not conform
to the tail recursive model. In the code of the method, the output statement
comes after the recursive call. Thus, the first time the output statement
executes is after all the recursive calls have been made. The first
output statement to print executes only when successive recursive calls
have reduced the first parameter to 0, and increased the second parameter
to the sum of all the values of the first parameter (when the initial call
is sum(n, 0) for some positive integer n).
public static void sum (int n, int s)
{
if (n > 0)
sum (n - 1, n + s);
System.out.println ("Sum at " + n + " is:" + (n + s));
}
And, here is the output produced when the method is called as: x(5, 0):
Sum at 0 is:15 Sum at 1 is:15 Sum at 2 is:14 Sum at 3 is:12 Sum at 4 is:9 Sum at 5 is:5
All our programs begin executing at the first statement of the main method. To begin executing the main method requires that the information defining the execution environment be stored in a data structure that we'll refer to as the execution stack. The stored information includes parameter and local variable values. Then, when a statement in main calls methodA, the run-time environment suspends execution of main, keeping track of what statement should be executed next when main resumes running, and creates another entry in the execution stack to store the environment information (parameters, local variables) for methodA. When methodA finishes executing, main can resume where it left off, using the stored information. But wait, what about methodB and methodC? The same mechanism applies. When methodA calls methodB,a new stack frame is created for methodB, "on top of" that for methodA, and then methodB begins running. When methodB calles methodC, methodB's status as the currently executing method is replaced by pushing a new entry onto the top of the execution stack, that for methodC. Assume that methodC does not call any other methods. What happens when it finishes executing? Now methodB can now continue executing. The stack frame for methodC is popped from the stack, and methodB resumes executing at the point that was stored when it was suspended. When methodB finishes, methodA can resume, through the same process. The system pops the stack again, restoring methodA to the currently executing top-of-stack position. Finally, when methodA finishes, main can resume, using the same mechanism.
The execution stack handles recursive method execution in the same way. The initial call of the method executes until the recursive call is encountered. Then the state information for the new copy of the recursive method is stored (pushed) onto the stack, and the first recursively called instance begins running. Assuming that it has not reached the base case, when the recursive call is encountered, the calling method is suspended, and the information for the next recursive call is added on the top of the stack. Notice that each recursive call gets it own storage for parameters and local variables when its stack frame is created and it starts executing. Thus there is no confusion over parameters and variables. The process continues until eventually, a call executes the base case, rather than the recursive path. Typically, it then finishes executing, its stack entry is popped off the stack and the immediately preceding copy can resume executing, with its restored parametes and local variables, and incorporating any changes produced by the recursive call that just finished. The process repeats until all the recursive calls have completed. At that point, whatever method called the recursive method resumes executing, with it's next statement.
| Stack
Time 0 |
Stack
Time 1 |
Stack
Time 2 |
Stack
Time 3 |
Stack
Time 4 |
Stack
Time 5 |
Stack
Time 6 |
| fact(0)
base case |
||||||
| fact(1)
return 1*fact(0) |
fact(1)
return 1*fact(0) |
|||||
| fact(2)
return 2*fact(1) |
fact(2)
return 2*fact(1) |
fact(2)
return 2*fact(1) |
||||
| fact(3)
return 3*fact(2) |
fact(3)
return 3*fact(2) |
fact(3)
return 3*fact(2) |
fact(3)
return 3*fact(2) |
|||
| fact(4)
return 4*fact(3) |
fact(4)
return 4*fact(3) |
fact(4)
return 4*fact(3) |
fact(4)
return 4*fact(3) |
fact(4)
return 4*fact(3) |
||
| fact(5)
return 5*fact(4) |
fact(5)
return 5*fact(4) |
fact(5)
return 5*fact(4) |
fact(5)
return 5*fact(4) |
fact(5)
return 5*fact(4) |
fact(5)
return 5*fact(4) |
|
| main
int f=fact(5); |
main
int f=fact(5); |
main
int f=fact(5); |
main
int f=fact(5); |
main
int f=fact(5); |
main
int f=fact(5); |
main
int f=fact(5); |
This part of the table shows the execution stack shrinking over time
as the base case is reached and recursive calls can begin to terminate,
with their stack frames being popped off the stack to allow the previous
call to execute. As each recursive call ends it returns a value to the
calling instance of the method, and its stack frames is popped.
| Stack
Time 7 |
Stack
Time 8 |
Stack
Time 9 |
Stack
Time 10 |
Stack
Time 11 |
Stack
Time 12 |
Stack
Time 13 |
| fact(0)
return 1 |
||||||
| fact(1)
return 1*fact(0) |
fact(1)
return 1*1=1 |
|||||
| fact(2)
return 2*fact(1) |
fact(2)
return 2*fact(1) |
fact(2)
return 2*1=2 |
||||
| fact(3)
return 3*fact(2) |
fact(3)
return 3*fact(2) |
fact(3)
return 3*fact(2) |
fact(3)
return 3*2=6 |
|||
| fact(4)
return 4*fact(3) |
fact(4)
return 4*fact(3) |
fact(4)
return 4*fact(3) |
fact(4)
return 4*fact(3) |
fact(4)
return 4*6=24 |
||
| fact(5)
return 5*fact(4) |
fact(5)
return 5*fact(4) |
fact(5)
return 5*fact(4) |
fact(5)
return 5*fact(4) |
fact(5)
return 5*fact(4) |
fact(5)
return 5*24=120 |
|
| main
int f=fact(5); |
main
int f=fact(5); |
main
int f=fact(5); |
main
int f=fact(5); |
main
int f=fact(5); |
main
int f=fact(5); |
main
int f=120; |
1 if n = 0
1 if n = 1
otherwise fib(n -1) + fib (n - 2)
Unfortunately, implementing this definition directly as a recursive method definition is not a good idea. It is extremely inefficient compared to implementations using alternative algorithms. Here's the definition of a recursive method to compute and return the fibonacci number for a non-negative integer n:
public static int fib (int n)
{
if (n == 0 || n == 1)
return 1;
else
return fib(n - 1) + fib (n - 2);
}
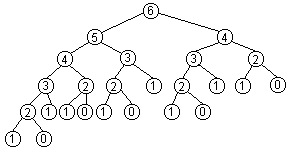
First, notice that this method is doubly tail recursive. By itself, that
is not necessarily a problem. However, think about what happens in a call
of the method as it is currently written. For example, the call fib(6)
calls fib(5), and when that completes, fib(4). But what
does fib(5) do? It recursively calls fib(4) and, when
that completes, fib(3). It should be apparent that this algorithm
will result in a great deal of duplicated work. The following figure illustrates
just how much.
A significantly more efficient sorting algorithm called Quick Sort uses quite a different strategy, one that leads naturally to a recursive implementation. The Quick Sort algorithm relies on two observations about the sorting process. One is that it would be preferable, when swapping, to swap over longer distances. The other, which leads to the recursive implementation, is that a divide and conquer approach can be applied to the sorting task. The goal at each step is to split the array into two parts such that each part is ordered with respect to the other. That is, all the values in one part are less than or equal to some partitioning or pivot value, while all the values in the other part are greater than or equal to the partitioning value. Then, the algorithm may be applied, recursively, to each of those partitions.
Here's a listing of the steps in the algorithm.
A Java program that contains a simple implementation of the Quick Sort
algorithm as a method and also a method with additional output added to
the quickSort() method to show a trace of the recursive calls
is available for viewing/download here.
If you would like a textual illustration of the operation of the recursive
quickSort() method, see the PowerPoint notes here.
Back to Contents
However, you should be aware that the idea of self-referencing definitions, as exemplified above by recursive methods, also is often applied to data structures, as well as to algorithms. If you take additional computing science/programming courses, you will encounter the ideas of linked lists and trees, data structures for which each element contains both data and one or more references to other elements. In a simple, singly-linked list, for example, each element contains data and a possible reference to an additional element. That reference can have either the special value null to indicate the list terminates, or a value that references another list element. Processing such a list might well involve a recursive algorithm that processes the current head of the list and recursively called on the tail. Perhaps that is the origin of the term tail recursion. Entire programming languages, like LISP, have been built around these ideas for structuring and processing data.
This section also includes an illustration based on a somewhat more complex problem, one that can be solved recursively, but one that does not employ simple tail recursion. The problem is a puzzle known as the Towers of Hanoi. Here is a brief description of the traditional presentation of the puzzle.
In a monastery in Benares India there are three diamond towers holding 64 disks made of gold. The disks are each of a different size and have holes in the middle so that they slide over the towers and sit in a stack. When they started, 1500 years ago, all 64 disks were all on the first tower arranged with the largest on the bottom and the smallest on the top. The monks' job is to move all of the disks to the third tower following these three rules:This description has inspired many variations, most of which are simple games in which the goal is to move a stack of n disks (where n is some positive integer much smaller than 64) from a source peg or tower to a destination peg or tower, following the rules outlined above, and using a third peg or tower as a "spare" for intermediate moves.The monks are very good at this after all this time and can move about 1 disk per second. When they complete their task, THE WORLD WILL END! The question is, how much time do we have left?
- Each disk sits over a tower except when it is being moved.
- No disk may ever rest on a smaller disk.
- Only one disk at a time may be moved.
Let's consider the problem of computing an optimal solution to the puzzle (minimal number of moves of disks) and then return to the issue of the End of the World.
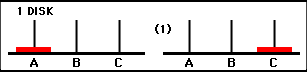
Here are lists of the minimal moves to solve the puzzle for 1 disk, 2 disks, and 3 disks. The accompanying illustrations are reproduced from the Math Forum: Ask Dr. Math FAQ. Here is a link to the description of the puzzle and solution from that source: Towers Info The versions of the puzzle for 1, 2, and 3 disks are presented both pictorially, and as lists of moves. After having a look at these examples, you should have some idea about the general pattern that allows a recursive solution to be programmed. The towers/pegs are labelled as A, B, and C in the illustrations.
Base Case: Move a "stack" consisting of 1 disk from peg A to peg C.
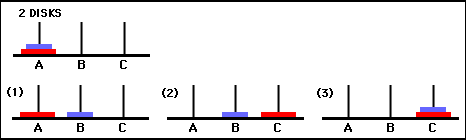
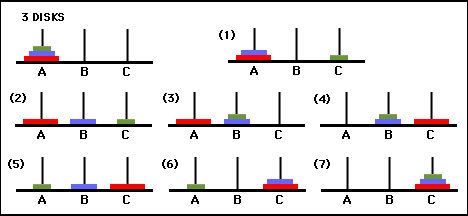
move a stack of N disks from A to C, following the rules, using B if N is 1 trivial, simply move the disk to C if N is 2 move the smaller disk to B move the larger disk to C then the smaller disk from B to C if N is 3 move the top 2 to B move the largest to C then move the top 2 from B to C for larger N, restate the problem in terms of N-1 and so on for 8 disks move 7 to the spare location then move the largest to the destination then move the stack of 7 to the destination to move 7 to their destination move 6 to the spare location then move the largest to the destination then move 6 to their destination and so on, until the problem is just to move 1, which can be done directlyOnce you've seen the the solution, it's not too difficult to develop a recursive method to display the solution for an arbitrary number of disks. Here are links to Java programs with recursive methods to solve the puzzle. In the first, here, the method just prints each individual move in the process. In the second, here, the code has been elaborated to keep track of the current state of the puzzle in array data structures to allow printing a simple graphical representation of the moves on the console screen.
Just in case you were worried about the imminent end of the world, here's some calming information.
Until recently I have believed, with my reference Dictionary of Mathematics, that the Tower of Hanoi puzzle is of ancient Indian origin, as the above rather widespread legend would also suggest. But it seems that it was actually invented from scratch probably together with the accompanying legend only in 1883 by the French mathematician Edouard Lucas. At least there is no known written record about the puzzle or the legend prior to 1883. M. Kolar, here