

More precisely: In a 3D scene consisting of a planar polygonal light source and a number of polyhedral objects (which have planar faces), define the direct primary irradiance as
0 1 /
B (x) = ---- | N(x) L(omega,x) d omega
pi /
V(x)
where x is a point on a face of the scene, V(x) is
the set of directions in which the light source is visible from
x, N(x) is the outward face normal at x,
L(omega,x) is a vector in direction omega with
magnitude equal to the light intensity in that direction, and d
omega is an infinitesimal solid angle.
Shadow boundaries correspond to discontinuities in B^0(x) and
in its first and second derivatives. These shadow boundaries form
lines and conic curves on the surfaces of the scene.
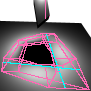
Examples are shown below, where pink lines are second derivative discontinuities (called D2 EV), yellow conic curves are also second derivative discontinuities (called D2 EEE), and blue lines are first derivative discontinuites (called D1).
Intensities are quantized in the images, resulting in obvious isolux contours. Pixel values have been jittered slightly to smooth the isolux contours. This is best viewed with 24-bit colour.
Please refer to the paper for a description of our discontinuity meshing algorithm, as well as references to much of the other work in discontinuity meshing. See also
 |
 |
|||
| Rendered | Rendered with mesh |
 |
 |
 |
 |
|||||||||
| Rendered | Rendered with mesh | Close up | Close up with mesh | |||||||||
 |
 |
|||||||||||
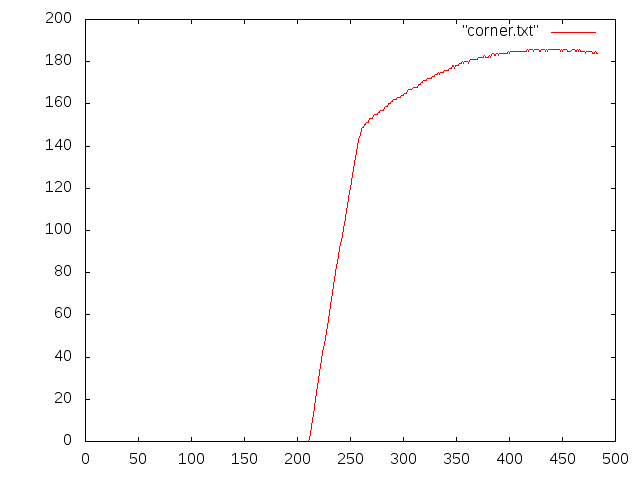
| Illumination across a horizontal line of the image | Illumination across a horizontal line of this image (to the right) |
Up to James Stewart's home page.